Le paradoxe
de Banach-Tarski

Dans le fascinant monde des mathématiques, parfois, la réalité et l'intuition s'évanouissent dans un tourbillon de paradoxes. L'un de ces mystères les plus perplexe est le paradoxe de Banach-Tarski. Dans cet article, nous explorerons ce phénomène intrigant, plongeant dans les concepts tordus de la décomposition et de la reconstitution, et examinant comment ce paradoxe a secoué les fondements de la géométrie et de la compréhension de l'espace.

L'énigme du paradoxe.

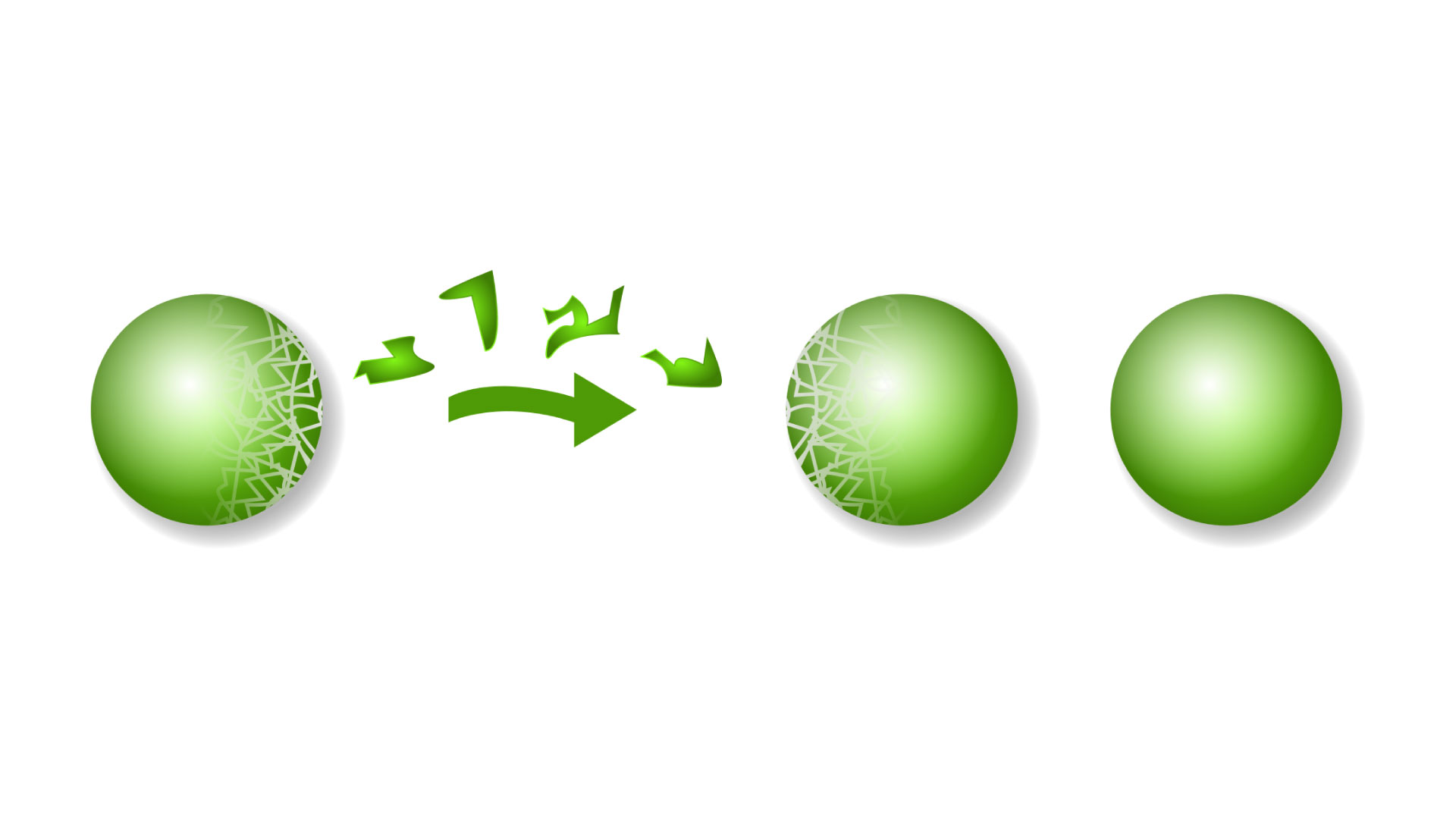
Le paradoxe de Banach-Tarski, formulé par les mathématiciens polonais Stefan Banach et Alfred Tarski en 1924, semble contredire notre compréhension commune de la géométrie et de la réalité. Il affirme que l'on peut diviser une sphère tridimensionnelle en un nombre fini de pièces, puis réassembler ces morceaux pour obtenir deux sphères identiques à l'originale.

La magie de la décomposition.

Ce paradoxe repose sur le concept étonnant que certaines collections de points dans l'espace, appelées ensembles non mesurables, ne peuvent pas être mesurées de manière conventionnelle en termes de volume. En exploitant ces propriétés étranges, les mathématiciens décomposent une sphère en sous-ensembles spécifiques, permettant ainsi leur réarrangement en deux entités identiques.

Les limites de l'intuition.

Le paradoxe de Banach-Tarski défie notre intuition profondément enracinée sur la conservation du volume. Il révèle que dans les domaines mathématiques avancés, la logique peut parfois produire des résultats en contradiction avec notre perception du monde réel. Cela souligne la distinction cruciale entre les mathématiques abstraites et les applications concrètes.

Des conséquences non physiques.

Bien que le paradoxe de Banach-Tarski puisse sembler incroyable, il est important de noter qu'il ne peut pas être réalisé dans le monde physique tel que nous le connaissons. Les propriétés spécifiques des ensembles mathématiques impliqués ne correspondent pas aux propriétés des objets réels. Cependant, ce paradoxe a suscité des discussions animées sur la nature de l'infini et les limites de notre compréhension de l'espace.

En conclusion, le paradoxe de Banach-Tarski nous rappelle que les mathématiques ne sont pas toujours conformes à notre vision du monde matériel. C'est une fenêtre intrigante sur les subtilités de l'infini et les façons étonnantes dont les idées abstraites peuvent défier nos intuitions les plus élémentaires. Bien que ce paradoxe puisse sembler éloigné de la réalité, il révèle néanmoins la puissance et la profondeur des concepts mathématiques qui continuent d'éclairer notre compréhension du cosmos.

Les mathématiques sont la porte et la clé des sciences... Les mathématiques ne mentent jamais. Un cercle n'est jamais un carré. - Alfred Tarski

Cette découverte lève le voile sur une énigme qui devrait donner du fil à retordre aux scientifiques. Une chose est sûre : les trous noirs n’ont pas fini de nous surprendre. Encore inconnus il y a quelques dizaines d’années, nous savons aujourd’hui qu’ils sont omniprésents dans l’univers, que leur taille peut être très différente de l’un à l’autre et qu’ils se dévorent entre eux. Cette nouvelle découverte vient mettre à mal plusieurs des grandes théoriques utilisées pour décrire la structure de l’univers, et notamment notre compréhension du fonctionnement de la gravité.

Je vous remercie d'avoir lu cet article et j'espère qu'il vous a plu, n'hésitez pas à vous abonner à ma newsletter pour ne pas rater les prochaines publications ainsi qu'à consulter ma chaîne YouTube ! (Abonnez-vous pour soutenir mon travail 😄)

À bientôt !