L'Hôtel de Hilbert :
où l'infini trouve une chambre ?

Dans le monde fascinant des mathématiques, il existe un endroit tout à fait unique et mystérieux : l'Hôtel de Hilbert. Bien qu'il ne s'agisse pas d'un lieu physique, cet établissement imaginaire propose une perspective intrigante sur le concept d'infini et sur la manière dont les mathématiciens jonglent avec des idées qui défient notre intuition. Dans cet article, nous ouvrirons les portes de cet hôtel étonnant, explorerons ses chambres infinies et plongerons dans la manière dont les paradoxes de l'infini y sont résolus.

Le concept de l'Hôtel de Hilbert.

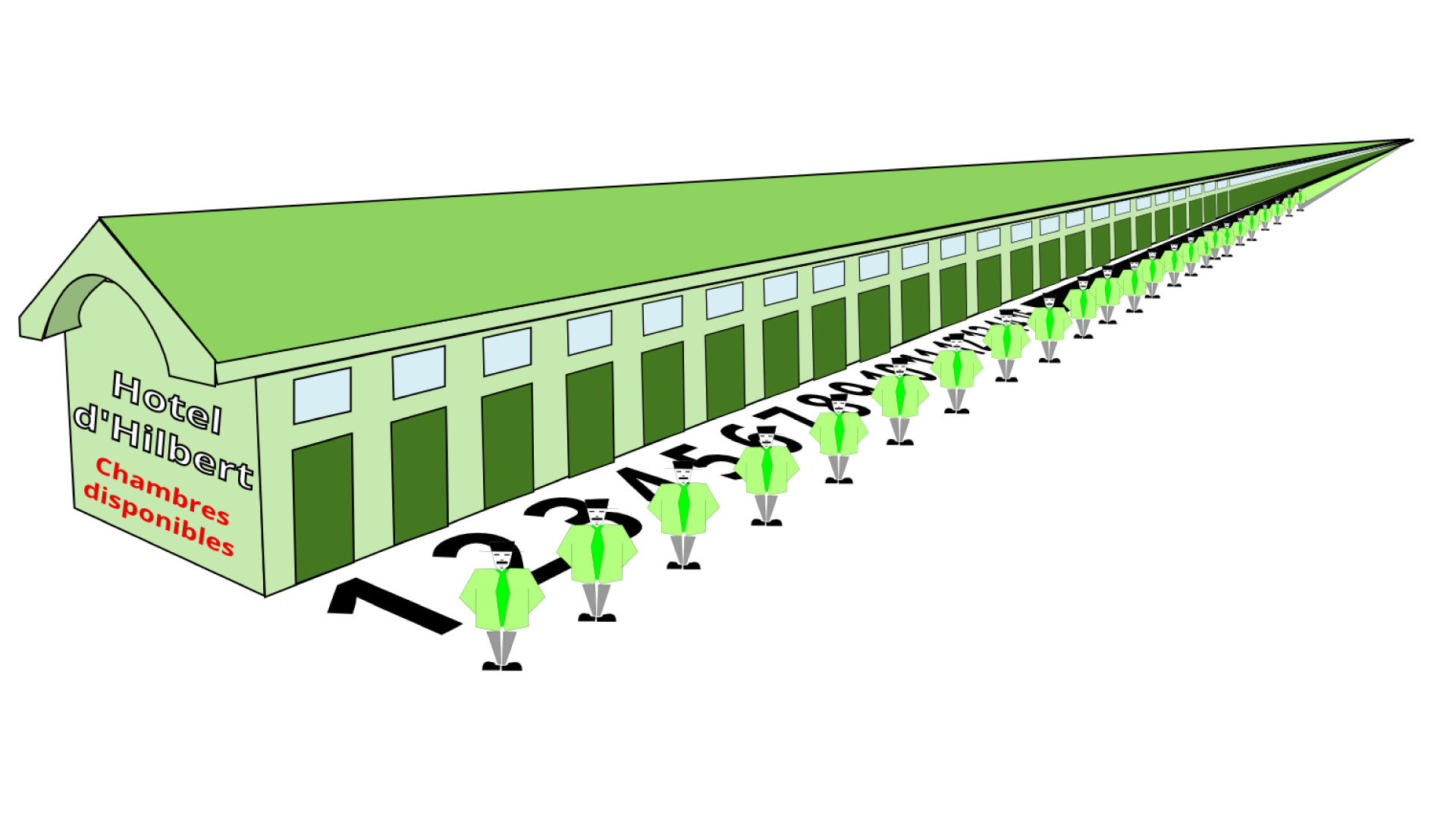
L'Hôtel de Hilbert est une invention mathématique conçue pour illustrer les propriétés fascinantes et parfois déconcertantes de l'infini. Imaginons un hôtel avec une infinité de chambres, numérotées 1, 2, 3, et ainsi de suite. Ce qui rend cet hôtel particulièrement étrange, c'est qu'il peut toujours accueillir de nouveaux invités, même s'il est déjà complet, en déplaçant les occupants actuels vers des chambres numérotées plus grandes.

L'invité infini et le paradoxe de Galilée.

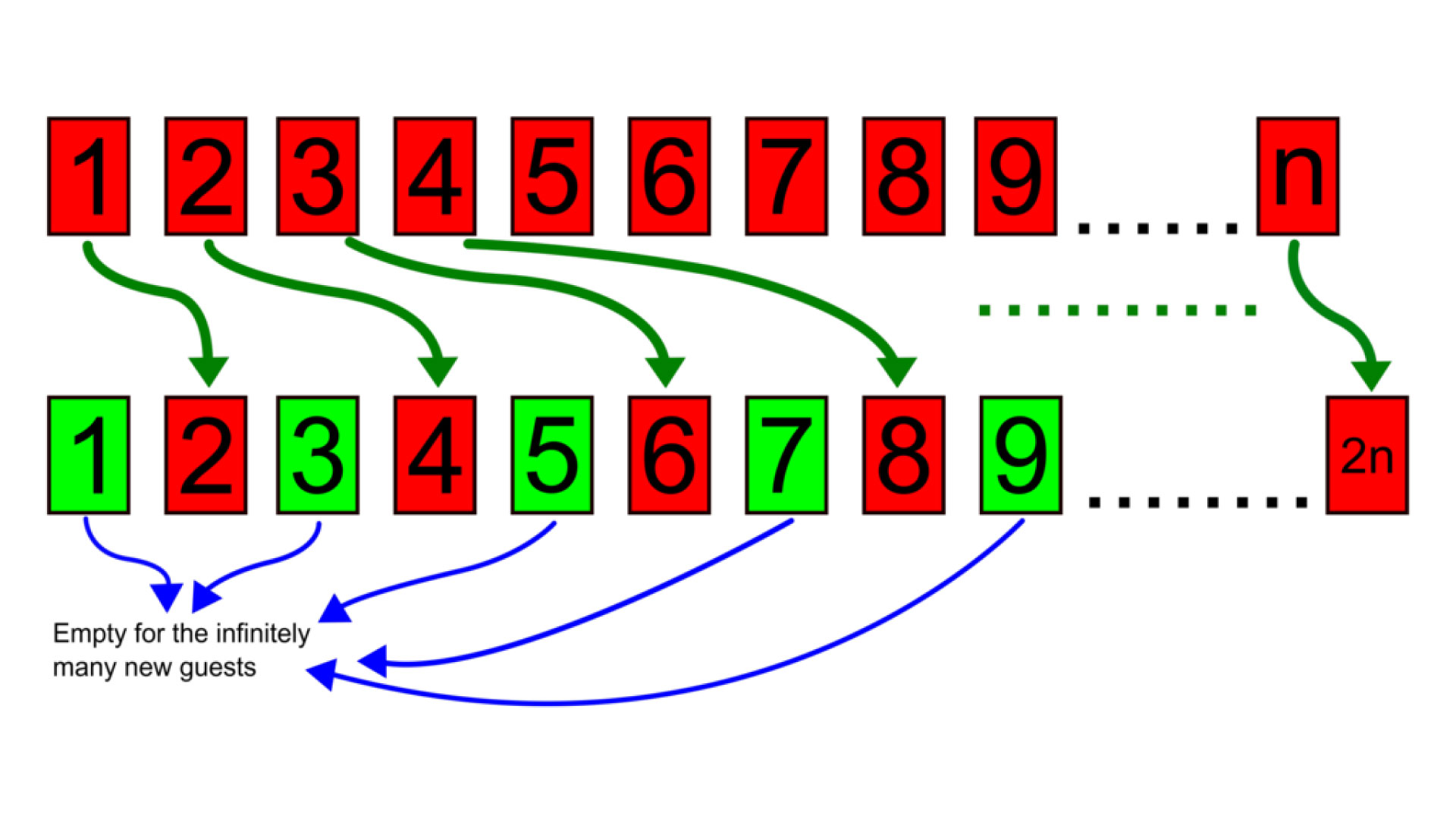
Supposons que l'Hôtel de Hilbert soit complet, avec un invité dans chaque chambre. Maintenant, imaginons un nouvel invité qui souhaite séjourner à l'hôtel. Le gérant peut facilement satisfaire cette demande en demandant à chaque invité actuel de se déplacer dans la chambre avec un numéro deux fois plus grand que la sienne. Ainsi, chaque chambre impaire restera occupée, tandis que les chambres paires accueilleront les nouveaux invités. Cette démonstration met en évidence comment l'infini peut être manipulé de manière surprenante.

L'infini + 1 : les nombres transfinis.

Le concept de l'Hôtel de Hilbert nous conduit également à explorer les nombres transfinis, introduits par le mathématicien allemand Georg Cantor. Ces nombres, tels que l'infini ω et au-delà, ont révolutionné la manière dont nous pensons à l'infini. Ils nous permettent de comparer et de mesurer différentes tailles d'ensembles infinis, une idée qui défie souvent notre intuition.

Résoudre les paradoxes de l'infini.

Bien que l'Hôtel de Hilbert puisse sembler énigmatique, il démontre en réalité comment les mathématiciens gèrent les paradoxes de l'infini en utilisant des concepts tels que la bijection et l'injection. Ces méthodes permettent de comprendre comment les ensembles infinis peuvent avoir des tailles égales ou différentes tout en respectant les règles mathématiques rigoureuses.

En conclusion, l'Hôtel de Hilbert est bien plus qu'une simple curiosité mathématique. Il nous invite à explorer les recoins fascinants de l'infini et à repousser les limites de notre pensée. Ce voyage dans l'inconnu mathématique nous rappelle que même les concepts les plus abstraits peuvent avoir des implications profondes dans la manière dont nous percevons et comprenons le monde qui nous entoure.

Je vous remercie d'avoir lu cet article et j'espère qu'il vous a plu, n'hésitez pas à vous abonner à ma newsletter pour ne pas rater les prochaines publications ainsi qu'à consulter ma chaîne YouTube ! (Abonnez-vous pour soutenir mon travail 😄)

À bientôt !